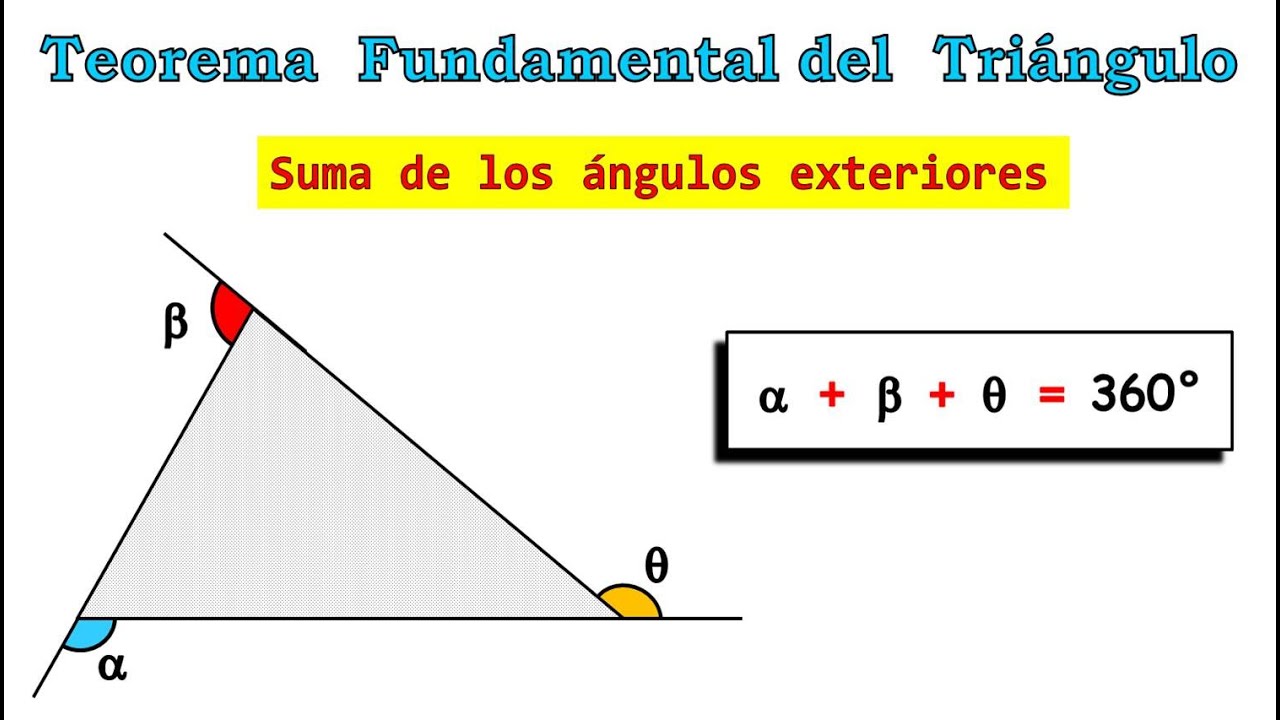
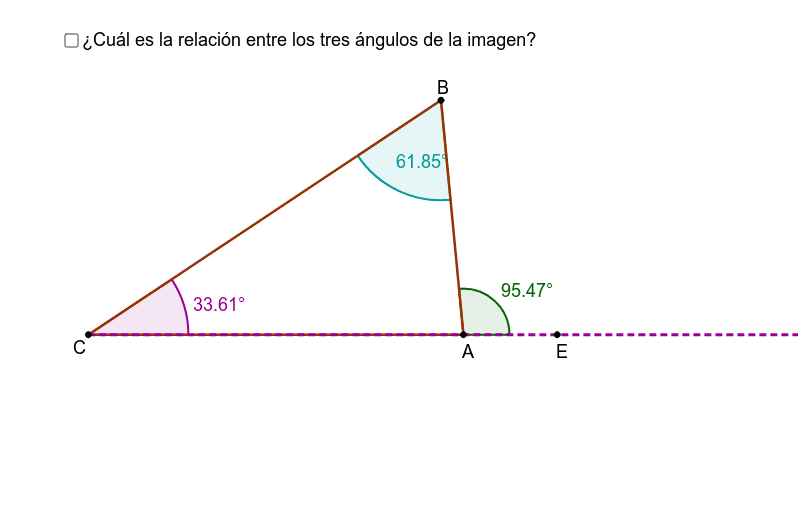
El teorema del ángulo exterior es la Proposición 1.16 en los Elementos de Euclides que dice lo siguiente:
Demostración
Lado: ABC es un triángulo, y ACD es un ángulo exterior al mismo.
Para probar: mACD = mABC mBAC (aquí, mACD denota la medida del ángulo ACD)
Prueba:
Referencias
- Faber, Richard L. (1983), Foundations of Euclidean and Non-Euclidean Geometry, New York: Marcel Dekker, Inc., ISBN 0-8247-1748-1 .
- Greenberg, Marvin Jay (1974), Euclidean and Non-Euclidean Geometries/Development and History, San Francisco: W.H. Freeman, ISBN 0-7167-0454-4 .
- Henderson, David W.; Taimiņa, Daina (2005), Experiencing Geometry/Euclidean and Non-Euclidean with History (3rd edición), Pearson/Prentice-Hall, ISBN 0-13-143748-8 .
- Venema, Gerard A. (2006), Foundations of Geometry, Upper Saddle River, NJ: Pearson Prentice Hall, ISBN 0-13-143700-3 .
- Wylie, Jr., C.R. (1964), Foundations of Geometry, New York: McGraw-Hill .
Enlaces externos
- Demostración del Teorema del ángulo exterior en hotmath.com
- Otra demostración del Teorema del ángulo exterior en Escuela Preparatoria "Gral. Lázaro Cárdenas"