Ecuación de la enana blanca de Chandrasekhar

En astrofísica, la ecuación de la enana blanca de Chandrasekhar es una ecuación diferencial ordinaria de valor inicial introducida por el astrofísico estadounidense de origen indio Subrahmanyan Chandrasekhar,^[1]​ en su estudio del potencial gravitatorio de estrellas enanas blancas completamente degeneradas. La ecuación es la siguiente^[2]​

$${\displaystyle {\frac {1}{\eta ^{2}}}{\frac {d}{d\eta }}\left(\eta ^{2}{\frac {d\varphi }{d\eta }}\right) (\varphi ^{2}-C)^{3/2}=0}$$

con condiciones iniciales

$${\displaystyle \varphi (0)=1,\quad \varphi '(0)=0}$$

dónde ${\displaystyle \varphi }$ representa la densidad de la enana blanca, ${\displaystyle \eta }$ es la distancia radial adimensional desde el centro y ${\displaystyle C}$ es una constante que está relacionada con la densidad de la enana blanca en el centro. El límite ${\displaystyle \eta =\eta _{\infty }}$ de la ecuación está definida por la condición

$${\displaystyle \varphi (\eta _{\infty })={\sqrt {C}}.}$$

tal que el rango de ${\displaystyle \varphi }$ es ${\displaystyle {\sqrt {C}}\leq \varphi \leq 1}$ . Esta condición equivale a decir que la densidad se vuelve nula en ${\displaystyle \eta =\eta _{\infty }}$ .

Obtención de la ecuación

A partir de la estadística cuántica de un gas de electrones completamente degenerado (esto es, aquel en el que todos los estados cuánticos de mínima energía están ocupados), la presión y la densidad de una enana blanca se obtienen en términos del momento máximo de los electrones ${\displaystyle p_{0}}$, Definiendo ${\displaystyle x=p_{0}/mc}$, la presión y la densidad del gas son ${\displaystyle P=Af(x)}$ y ${\displaystyle \rho =Bx^{3}}$, respectivamente, donde

$${\displaystyle {\begin{aligned}&A={\frac {\pi m_{e}^{4}c^{5}}{3h^{3}}}=6.02\times 10^{21}{\text{ Pa}},\\&B={\frac {8\pi }{3}}m_{p}\mu _{e}\left({\frac {m_{e}c}{h}}\right)^{3}=9.82\times 10^{8}\mu _{e}{\text{ kg/m}}^{3},\\&f(x)=x(2x^{2}-3)(x^{2} 1)^{1/2} 3\sinh ^{-1}x,\end{aligned}}}$$

donde ${\displaystyle \mu _{e}}$ es el peso molecular medio del gas, y ${\displaystyle h}$ es la altura de un pequeño cubo de gas con sólo dos estados posibles.

Sustituyendo esto en la ecuación de equilibrio hidrostático

$${\displaystyle {\frac {1}{r^{2}}}{\frac {d}{dr}}\left({\frac {r^{2}}{\rho }}{\frac {dP}{dr}}\right)=-4\pi G\rho }$$

dónde ${\displaystyle G}$ es la constante de gravitación universal y ${\displaystyle r}$ es la distancia radial, obtenemos

$${\displaystyle {\frac {1}{r^{2}}}{\frac {d}{dr}}\left(r^{2}{\frac {d{\sqrt {x^{2} 1}}}{dr}}\right)=-{\frac {\pi GB^{2}}{2A}}x^{3}}$$

y definiendo ${\displaystyle y^{2}=x^{2} 1}$, tenemos

$${\displaystyle {\frac {1}{r^{2}}}{\frac {d}{dr}}\left(r^{2}{\frac {dy}{dr}}\right)=-{\frac {\pi GB^{2}}{2A}}(y^{2}-1)^{3/2}}$$

Si denotamos la densidad en el origen como ${\displaystyle \rho _{o}=Bx_{o}^{3}=B(y_{o}^{2}-1)^{3/2}}$, podemos definir una escala adimensional

$${\displaystyle r=\left({\frac {2A}{\pi GB^{2}}}\right)^{1/2}{\frac {\eta }{y_{o}}},\quad y=y_{o}\varphi }$$

tal que

$${\displaystyle {\frac {1}{\eta ^{2}}}{\frac {d}{d\eta }}\left(\eta ^{2}{\frac {d\varphi }{d\eta }}\right) (\varphi ^{2}-C)^{3/2}=0}$$

dónde ${\displaystyle C=1/y_{o}^{2}}$ . En otras palabras, una vez resuelta la ecuación anterior, la densidad es

$${\displaystyle \rho =By_{o}^{3}\left(\varphi ^{2}-{\frac {1}{y_{o}^{2}}}\right)^{3/2}.}$$

Podemos entonces calcular la masa interior dentro del radio adimensional ${\displaystyle \eta }$,

$${\displaystyle M(\eta )=-{\frac {4\pi }{B^{2}}}\left({\frac {2A}{\pi G}}\right)^{3/2}\eta ^{2}{\frac {d\varphi }{d\eta }}.}$$

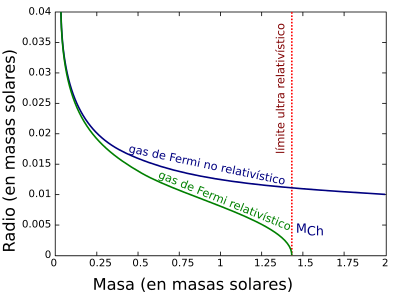
La relación radio-masa de las enana blanca suele representarse en el plano ${\displaystyle \eta _{\infty }}$ - ${\displaystyle M(\eta _{\infty })}$ .

Solución cerca del origen

En un entorno del origen, ${\displaystyle \eta \ll 1}$, Chandrasekhar obtuvo una expansión asintótica, dada por

$${\displaystyle {\begin{aligned}\varphi ={}&1-{\frac {q^{3}}{6}}\eta ^{2} {\frac {q^{4}}{40}}\eta ^{4}-{\frac {q^{5}(5q^{2} 14)}{7!}}\eta ^{6}\\[6pt]&{} {\frac {q^{6}(339q^{2} 280)}{3\times 9!}}\eta ^{8}-{\frac {q^{7}(1425q^{4} 11346q^{2} 4256)}{5\times 11!}}\eta ^{10} \cdots \end{aligned}}}$$

donde ${\displaystyle q^{2}=C-1}$ . También obtuvo soluciones numéricas en el rango ${\displaystyle C=0.01-0.8}$ .

Ecuación para densidades centrales pequeñas

Cuando la densidad central ${\displaystyle \rho _{o}=Bx_{o}^{3}=B(y_{o}^{2}-1)^{3/2}}$ es pequeña, la ecuación se puede reducir a una ecuación de Lane-Emden introduciendo

$${\displaystyle \xi ={\sqrt {2}}\eta ,\qquad \theta =\varphi ^{2}-C=\varphi ^{2}-1 x_{o}^{2} O(x_{o}^{4})}$$

para obtener a primer orden la siguiente ecuación

$${\displaystyle {\frac {1}{\xi ^{2}}}{\frac {d}{d\xi }}\left(\xi ^{2}{\frac {d\theta }{d\xi }}\right)=-\theta ^{3/2}}$$

con las condiciones ${\displaystyle \theta (0)=x_{o}^{2}}$ y ${\displaystyle \theta '(0)=0}$ . Nótese que, aunque la ecuación se reduce a la ecuación de Lane-Emden con índice politrópico ${\displaystyle 3/2}$, la condición inicial no es la de la ecuación de Lane-Emden.

Masa limitante para grandes densidades centrales

Cuando la densidad central es grande, es decir, ${\displaystyle y_{o}\rightarrow \infty }$ (o equivalententemente ${\displaystyle C\rightarrow 0}$), la ecuación se reduce a

$${\displaystyle {\frac {1}{\eta ^{2}}}{\frac {d}{d\eta }}\left(\eta ^{2}{\frac {d\varphi }{d\eta }}\right)=-\varphi ^{3}}$$

con condiciones ${\displaystyle \varphi (0)=1}$ y ${\displaystyle \varphi '(0)=0}$ . Esta es exactamente la ecuación de Lane-Emden con índice politrópico ${\displaystyle 3}$. Nótese que en este límite de grandes densidades centrales, el radio

$${\displaystyle r=\left({\frac {2A}{\pi GB^{2}}}\right)^{1/2}{\frac {\eta }{y_{o}}}}$$

tiende a cero. Sin embargo, la masa de la enana blanca tiende a un límite finito,

$${\displaystyle M\rightarrow -{\frac {4\pi }{B^{2}}}\left({\frac {2A}{\pi G}}\right)^{3/2}\left(\eta ^{2}{\frac {d\varphi }{d\eta }}\right)_{\eta =\eta _{\infty }}=5.75\mu _{e}^{-2}M_{\odot }.}$$

El límite de Chandrasekhar se deriva de este límite.

Véase también

• Ecuación de Tolman-Oppenheimer-Volkoff
• Límite de Chandrasekhar

Referencias