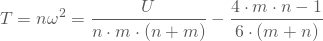Criterio de Cramér-von Mises

En estadística el criterio de Cramér-von Mises se emplea para juzgar la bondad de una función de distribución acumulada ${\displaystyle F^{*}}$ comparada con una función de distribución empírica ${\displaystyle F_{n}}$, o para comparar dos distribuciones empíricas. También se utiliza como parte de otros algoritmos, tal como la estimación de la distancia mínima. Se define como:

${\displaystyle \omega ^{2}=\int _{-\infty }^{\infty }[F_{n}(x)-F^{*}(x)]^{2}\,\mathrm {d} F^{*}(x)}$

Aplicándolo a una única muestra, ${\displaystyle F^{*}}$ es la distribución teórica y ${\displaystyle F_{n}}$ es la empírica. Alternativamente las dos distribuciones pueden ser estimadas empíricamente; esto se conoce como un caso de dos muestras.

El criterio lleva los apellidos de Harald Cramér y Richard Edler von Mises, quienes fueron los primeros en exponerlo entre los años 1928-1930. La generalización de las dos muestras es obra de Theodore Wilbur Anderson.^[1]​

El criterio es una alternativa al test de Kolmogorov-Smirnov.

Test de Cramér-von Mises (una muestra)

Sean ${\displaystyle x_{1},x_{2},\cdots ,x_{n}}$ los valores observados, en orden creciente. Entonces el estadístico es^[1]​^{: 1153 [2]}​

${\displaystyle T=n\omega ^{2}={\frac {1}{12n}} \sum _{i=1}^{n}\left[{\frac {2i-1}{2n}}-F(x_{i})\right]^{2}.}$

Si este valor es mayor que el valor tabulado, se puede rechazar la hipótesis de que los datos provienen de la distribución ${\displaystyle F}$

Test de Watson

Una versión modificada del criterio es el test de Watson,^[3]​ el cual usa el estadístico U², donde^[2]​

${\displaystyle U^{2}=T-n({\bar {F}}-{\tfrac {1}{2}})^{2},}$

donde

${\displaystyle {\bar {F}}={\frac {1}{n}}\sum F(x_{i}).}$

Test de Cramér–von Mises test (dos muestras)

Sean ${\displaystyle x_{1},x_{2},\cdots ,x_{N}}$ y ${\displaystyle y_{1},y_{2},\cdots ,y_{M}}$ los valores observados en la primera y segunda muestra respectivamente, en orden creciente. Sean ${\displaystyle r_{1},r_{2},\cdots ,r_{N}}$ los rangos de x en la muestra combinada, y sean ${\displaystyle s_{1},s_{2},\cdots ,s_{M}}$ los rangos de y en la muestra combinada. Anderson^[1]​^: 1149 muestra que

${\displaystyle T=N\omega ^{2}={\frac {U}{NM(N M)}}-{\frac {4MN-1}{6(M N)}}}$

donde U se define como

${\displaystyle U=N\sum _{i=1}^{N}(r_{i}-i)^{2} M\sum _{j=1}^{M}(s_{j}-j)^{2}}$

Si el valor de T es mayor que los valores tabulados,^[1]​^{: 1154–1159} se puede rechazar la hipótesis de que las dos muestras provienen de la misma distribución. Esto implica que no hay duplicados en ${\displaystyle x}$, ${\displaystyle y}$, y en las secuencias ${\displaystyle r}$. Por tanto ${\displaystyle x_{i}}$ es única, y su rango es ${\displaystyle i}$ en ${\displaystyle x_{1},...x_{N}}$. Si hay duplicados, y ${\displaystyle x_{i}}$ en ${\displaystyle x_{j}}$ son valores idénticos, donde se puede utilizar el enfoque del medio rango^[4]​ método: asignar a cada duplicado un rango de ${\displaystyle (i j)/2}$. En las ecuaciones precedentes, en las expresiones ${\displaystyle (r_{i}-i)^{2}}$ y ${\displaystyle (s_{j}-j)^{2}}$, los duplicados pueden alterar las cuatro variables ${\displaystyle r_{i}}$, ${\displaystyle i}$, ${\displaystyle s_{j}}$, y ${\displaystyle j}$.

Referencias

Bibliografía

• Anderson, TW (1962). «On the Distribution of the Two-Sample Cramer–von Mises Criterion» (PDF). The Annals of Mathematical Statistics (Institute of Mathematical Statistics) 33 (3): 1148-1159. ISSN 0003-4851. doi:10.1214/aoms/1177704477. Consultado el 12 de junio de 2009. 
• M. A. Stephens (1986). «Tests Based on EDF Statistics». En D'Agostino, R.B. and Stephens, M.A., ed. Goodness-of-Fit Techniques. New York: Marcel Dekker. ISBN 0-8247-7487-6. 
• Pearson, E.S., Hartley, H.O. (1972) Biometrika Tables for Statisticians, Volume 2, CUP. ISBN 0-521-06937-8 (page 118 and Table 54)
• Ruymgaart, F. H., (1980) "A unified approach to the asymptotic distribution theory of certain midrank statistics". In: Statistique non Parametrique Asymptotique, 1±18, J. P. Raoult (Ed.), Lecture Notes on Mathematics, No. 821, Springer, Berlín.
• Watson, G.S. (1961) "Goodness-Of-Fit Tests on a Circle", Biometrika, 48 (1/2), 109-114

Lecturas

• Xiao, Y.; A. Gordon; A. Yakovlev (enero de 2007). «A C Program for the Cramér–von Mises Two-Sample Test» (PDF). Journal of Statistical Software (American Statistical Association) 17 (8). ISSN 1548-7660. OCLC 42456366. Consultado el 12 de junio de 2009. 

Enlaces externos

• C-vM Two Sample Test (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última). (Documentación para llevar a cabo el test usando R
• Table of Critical values for 1 sample CvM test